
문제
박성원은 이 문제를 풀지 못했다.
서로 다른 정수로 이루어진 집합이 있다. 이 집합의 순열을 합치면 큰 정수 하나를 만들 수 있다. 예를 들어, {5221,40,1,58,9}로 5221401589를 만들 수 있다. 합친수가 정수 K로 나누어 떨어지는 순열을 구하는 프로그램을 작성하시오.
하지만, 박성원은 이 문제를 풀지 못했다.
따라서 박성원은 그냥 랜덤하게 순열 하나를 정답이라고 출력하려고 한다. 이 문제에는 정답이 여러 개 있을 수도 있고, 박성원이 우연히 문제의 정답을 맞출 수도 있다.
박성원이 우연히 정답을 맞출 확률을 분수로 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 집합의 수의 개수 N이 주어진다. N은 15보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 집합에 포함된 수가 주어진다. 각 수의 길이는 길어야 50인 자연수이다. 마지막 줄에는 K가 주어진다. K는 100보다 작거나 같은 자연수이다.
출력
첫째 줄에 정답을 기약분수 형태로 출력한다. p/q꼴로 출력하며, p는 분자, q는 분모이다. 정답이 0인 경우는 0/1로, 1인 경우는 1/1로 출력한다.
https://www.acmicpc.net/problem/1086
1086번: 박성원
첫째 줄에 정답을 기약분수 형태로 출력한다. p/q꼴로 출력하며, p는 분자, q는 분모이다. 정답이 0인 경우는 0/1로, 1인 경우는 1/1로 출력한다.
www.acmicpc.net
접근
숫자를 계속 붙여 K로 나눈 나머지가 0인 숫자의 개수를 찾고, 숫자를 만들 수 있는 모든 경우의 수로 나눈 값을 기약분수 형태로 출력해야 합니다.
1. 나머지 계산
먼저 나머지를 계산하는 방법 먼저 구해보겠습니다.
엥? 나머지야 %연산자를 사용하면 되는 것 아니겠습니까?
하지만 각 숫자의 최대 자리수가 50자리가 됩니다.
자바의 Long형 최대값은 9,223,372,036,854,775,807 으로 19자리밖에 되지 않습니다.
따라서 나머지를 구하는 방법은
1) BigInteger 클래스를 사용하거나
2) 최대자리수에서 순차적으로 계산하는 방법 을 사용하면 되겠습니다.
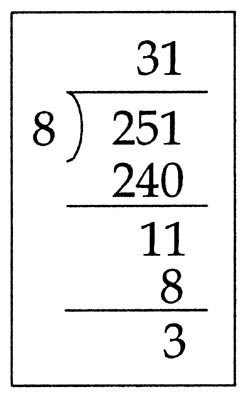
2)번의 경우, 어릴 때 하던 세로 나눗셈의 방식과 비슷합니다.
가장 큰 자릿수의 숫자를 k로 나누고, 나머지에 10을 곱한 뒤 다음 자릿수 숫자를 가져옵니다.
이 숫자를 또 k로 나누고, 다음 숫자를 가져옵니다...
이 과정을 1의 자리 숫자까지 반복하고, 남은 나머지가 최종 나머지입니다.
2. 여러 숫자가 붙은 나머지 계산
n1 이라는 수를 k로 나눈 나머지의 값이 r1 이라고 가정하겠습니다.
만약 n1에 n2라는 숫자가 붙는다면 (n1+""+n2), 이를 k로 나눈 나머지는 어떻게 될까요?
1-2)의 과정을 생각해보면 n1의 결과값이 r1이 남습니다.
이 숫자 뒤에 n2라는 숫자가 붙고, 이 숫자를 이용해 나머지를 계속 계산해줍니다.
결국, (r1+""+n2) 라는 숫자를 k로 나눈 나머지 값과 같다는 것을 알 수 있습니다.
3. 모든 경우의 수 탐색
n의 최대 개수는 15개이므로 이는 15!=1307674368000 입니다.
13조가 넘는 값임이므로 모든 경우를 탐색하기에는 오랜 시간이 걸릴것입니다.
이를 해결하기 위해 메모라이제이션 방법을 사용할 것입니다.
비트마스크를 이용하여 방문한 지점을 표시합니다.
우리가 구해야하는 값은 나머지임으로 합친 숫자의 값은 버리고 나머지만을 기록합니다.
dp를 이용하여 이전 계산값을 활용합니다.
dp[bitmask][x]는
"현재 방문지점(bitmask)에서 나머지가 x라면 아직 방문하지 않은 지역을 방문했을 때, k로 완성된 숫자를 나누면 0인 개수"
를 뜻합니다.
만약 해당 지점을 방문했을 때, 이미 값이 있다면 그대로 사용하고
값이 아직 설정되지 않았다면
(x+""+미방문 지역의 숫자)의 나머지를 새나머지로 하여
dp[새방문지점][새나머지]를 재귀로 탐색합니다.
만약 모든 점을 방문한 경우, 나머지가 0이라면 1, 아니라면 0을 리턴합니다.
4. 기약 분수 출력
정수를 나열하는 경우의 수는 n! 입니다.
나열한 수 중 K의 나머지가 0인 개수를 x라고 한다면
x와 n!의 최소공배수를 gcd라고 한다면
(x/gcd) / (n!/gcd) 를 출력합니다.
구현
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
//https://www.acmicpc.net/problem/1086
static String[] Nums;
static int K,N;
static int MaxBitmask;
static long[][] Dp;
static int[][] Mods;
//dp를 이용하여 이미 계산한 값을 사용함
public static long dp(int bitmask, int mod) {
//이미 방문한 경우, dp값 리턴
if(Dp[bitmask][mod]!=-1) {
return Dp[bitmask][mod];
}
//모든 점을 방문한 경우, mod가 0이면 1, 아니면 0
if(bitmask==MaxBitmask) {
return mod==0?1:0;
}
//나머지가 0인 개수
long count = 0;
//아직 미방문 idx 조사
for(int i=0;i<N;i++) {
int idx = 1<<i;
//아직 방문하지 않았다면
if((bitmask&idx)==0) {
//방문여부 표시, mod 업데이트 하여 재귀한 값을 추가
count+=dp(bitmask|idx, getMod(i, mod));
}
}
//dp에 count 저장하고 리턴
return Dp[bitmask][mod]=count;
}
//나머지 구하기
public static int getMod(int idx, int mod) {
if(Mods[idx][mod]!=-1) return Mods[idx][mod];
int curr = mod;
int length = Nums[idx].length();
for(int i=0;i<length;i++) {
curr*=10; //10의 자리로 증가
curr+=(Nums[idx].charAt(i)-'0'); //1의 자리 더하기
curr%=K; //K로 나눈 나머지 값
}
//나머지 출력
return Mods[idx][mod]=curr;
}
//최대공약수 구하기
public static long getGcd(long n, long m) {
if(m==0) return n;
return getGcd(m, n%m);
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine()); //집합수
Nums = new String[N]; //집합을 저장할 배열
//배열 넣기
for(int i=0;i<N;i++) {
Nums[i]=br.readLine();
}
//나눌 수 K
K=Integer.parseInt(br.readLine());
//모든 지점 방문 비트마스크
MaxBitmask = (1<<N)-1;
//[방문지점][나머지] 기록을 위한 dp
Dp=new long[1<<N][K];
//[배열 순서][나머지]에 따른 나머지 값 계산 배열
Mods = new int[N][K];
//나머지배열과 dp -1로 초기화
for(int j=0;j<K;j++) {
for(int i=0;i<N;i++) {
Mods[i][j]=-1;
}
for(int i=0;i<=MaxBitmask;i++) {
Dp[i][j]=-1;
}
}
//k로 나눈 나머지가 0인 수 계산 (모든 점 미방문, 나머지 0)
long answer = dp(0, 0);
//0이면 0/1 출력
if(answer==0) {
System.out.println("0/1");
//0이 아니면 최대공약수를 이용하여 기약분수형태로 출력
}else {
//팩토리얼, 모든 경우의 수 계산
long fac = 1;
for(int i=2;i<=N;i++) {
fac*=i;
}
//최대 공약수
long gcd = getGcd(fac, answer);
//기약분수 출력
System.out.println(answer/gcd+"/"+fac/gcd);
}
br.close();
}
}dp뿐만 아니라 나머지를 구하는 경우에도 메모라이제이션을 사용했습니다.
(그냥 사용하니 시간초과가 발생했습니다)
'알고리즘' 카테고리의 다른 글
| [백준] 2559번: 수열 Java (0) | 2022.05.31 |
|---|---|
| [백준] 17404번: RGB거리2 Java (0) | 2022.05.30 |
| [백준] 11779번: 최소비용 구하기 2 Java (0) | 2022.05.26 |
| [백준] 1086번: 부분합 Java (0) | 2022.05.24 |
| [프로그래머스] 2019 KAKAO BLIND RECRUITMENT : 무지의 먹방 라이브 Java (0) | 2022.05.18 |




댓글